Норм а льно распредел е ня, одне з найважливіших розподілів ймовірностей. Термін «Н. р. »застосовують як по відношенню до розподілів ймовірностей випадкових величин, так і по відношенню до спільних розподілів ймовірностей декількох випадкових величин (т. е. до распредсленіям випадкових векторів).
Розподіл ймовірностей випадкової величини Х називається нормальним, якщо воно має щільність ймовірності
. (*)
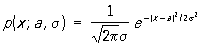Сімейство Н. р. (*) Залежить, т. О., Від двох параметрів а і s. При цьому математичне очікування Х одно а, дисперсія Х дорівнює s 2. Крива Н. р. у = р (х; а, s) симетрична щодо ординати, що проходить через точку х = а, і має в цій точці єдиний максимум, рівний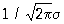 
. Зі зменшенням s крива Н. р. стає все більш і більш гостровершинності (див. рис.). Зміна а при постійному s не міняє форму кривої, а викликає лише її зсув по осі абсцис. Площа, укладена під кривою Н. р., Завжди дорівнює одиниці. При a = 0, s = 1 соответствуюших функція розподілу дорівнює
.
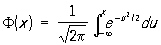У загальному випадку функція розподілу Н. р. (*) F (х; а, s) може бути обчислена за формулою F (x; а, s) = Ф (t), де t = (х - а) / s. Для функції Ф (t) (і кількох її похідних) складені обширні таблиці. Для Н. р. вірогідність нерівності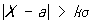 
, Що дорівнює 1 Ф (k) + Ф (- k), убуває досить швидко з ростом k (див. Таблицю).
k
1
0,31731
2
0,04550
3
0,00269
4
0,00006
У багатьох практичних питаннях при розгляді Н. р. нехтують тому можливістю відхилень від а, що перевищують 3 s, - т. зв. правило трьох сигма (відповідна ймовірність, як видно з таблиці, менше 0,003). Ймовірне відхилення для Н. р. одно 0,67449 s.
Н. р. зустрічається у великій кількості додатків. З давніх-давен відомі спроби пояснення цієї обставини. Теоретичне обґрунтування виняткової ролі Н. р. дають граничні теореми теорії ймовірностей (див. також Лапласа теорема , Ляпунова теорема ). Якісно відповідний результат може бути пояснено таким чином: Н. р. служить хорошим наближенням кожен раз, коли розглянута випадкова величина являє собою суму великого числа незалежних випадкових величин, максимальна з яких мала в порівнянні зі всією сумою.
Н. р. може з'являтися також як точне рішення деяких завдань (в рамках прийнятої математичної моделі явища). Така ситуація в теорії випадкових процесів (В одній з основних моделей броунівського руху ). Класичні приклади виникнення Н. р. як точного належать К. Гауса (Закон розподілу помилок спостереження) і Дж. Максвеллові (Закон розподілу швидкостей молекул).
Спільне розподіл кількох випадкових величин X 1, X 2, ..., X s називається нормальним (багатовимірним нормальним), якщо відповідна щільність ймовірності має вигляд:
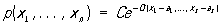, де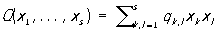 
,
qk, l = ql, k - позитивно певна квадратична форма. Постійна З визначається з того умови, що інтеграл від р по всьому простору дорівнює 1. Параметри a1, ..., as рівні математичним очікуванням X1, ..., Xs відповідно, а коефіцієнт qk, l можуть бути виражені через дисперсії s 1 2 , ..., s s 2 цих величин і коефіцієнт кореляції s k, l між Xk і Xl. Загальна кількість параметрів, які задають Н. р., Так само
(S + 1) (s + 2) / 2 - 1
і швидко росте з ростом s (воно дорівнює 2 при s = 1, 20 при s = 5 і 65 при s = 10). Багатовимірне Н. р. є основною моделлю статистичного аналізу багатовимірного . Воно використовується також в теорії випадкових процесів (де розглядають також Н. р. В нескінченновимірних просторах).
Щодо питань, пов'язаних з оцінкою параметрів Н. р. за результатами спостережень, див. статті малі вибірки і несмещенная оцінка . Про перевірку гіпотези нормальності см. непараметричні методи (В математичній статистиці).
Літ. см. при ст. розподілу .
Ю. В. Прохоров.
Криві щільності нормального розподілу для різних значень параметрів а і s: I. а = 0, s = 2,5; II. a = 0, s = 1; III. a = 0, s = 0,4; IV. a = 3, s = 1.
<
